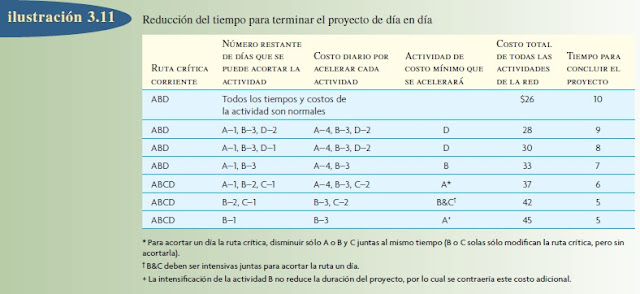
El supuesto básico del programa de costos mínimos es que existe una relación entre el tiempo para terminar una actividad y el costo de un proyecto. Por un lado, acelerar una actividad cuesta dinero y, por el otro, sostener (o prolongar) el proyecto también cuesta dinero. Los costos asociados a acelerar las actividades se llaman costos directos de las actividades y se suman al costo directo del proyecto. Algunos pueden estar relacionados con el trabajo, como las horas extra, la contratación de más trabajadores y el traslado de trabajadores procedentes de otros trabajos, otros están relacionados con los recursos, como la compra o el arrendamiento de equipamiento adicional o más eficiente y el uso de instalaciones adicionales de apoyo.
Los costos asociados a sostener el proyecto se llaman costos indirectos del proyecto: gastos fijos, instalaciones y costos de oportunidad de los recursos y, en ciertas situaciones contractuales, los costos de penalización o los pagos de incentivos que se pierden. Dado que los costos directos de las actividades y los costos indirectos del proyecto son costos contrarios que dependen del tiempo, el problema de su programación depende en esencia de encontrar la duración del proyecto que minimiza su suma o, en otras palabras, de encontrar el punto óptimo en un equilibrio de tiempo-costo.
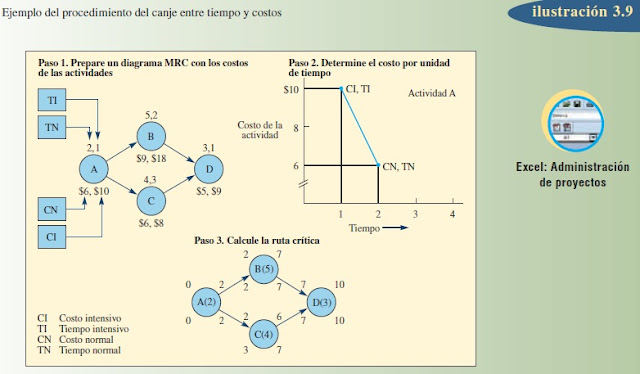
El procedimiento para encontrar este punto consiste en los siguientes cinco pasos y se explica utilizando la red simple de cuatro actividades que presenta la ilustración 3.9. Suponga que los costos indirectos permanecen constantes durante ocho días y que, a continuación, incrementan a un ritmo de 5 dólares por día.
1. Prepare un diagrama de red tipo MRC.
Para cada actividad, este diagrama debe enumerar:
a) El costo normal (CN): los costos más bajos esperados para la actividad. (Se trata de las cifras de costos más bajas que se presentan bajo cada nodo en la ilustración 3.9.)
b) El tiempo normal (TN): el tiempo asociado a cada costo normal.
c) El tiempo intensivo (TI): el tiempo más breve posible de cada actividad.
d) El costo intensivo (CI): el costo asociado a cada tiempo intensivo.
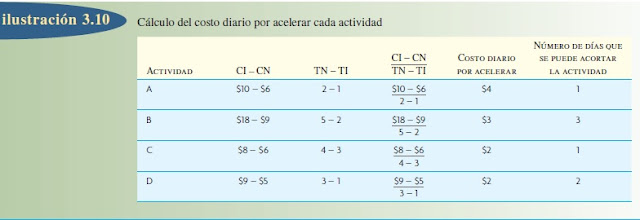
2. Determine el costo por unidad de tiempo (suponga días) para acelerar cada actividad.
La relación entre el tiempo y el costo de la actividad se puede representar gráficamente trazando las coordenadas CI y TI y conectándolas con las coordenadas CN y TN mediante una línea cóncava, convexa o recta, o de alguna otra forma, dependiendo de la estructura real del costo del desempeño de la actividad, como en la ilustración 3.9. Para la actividad A, se supone una relación lineal entre el tiempo y el costo. Este supuesto es común en la práctica y sirve para derivar el costo por día por acelerar las cosas porque este valor se puede encontrar directamente tomando la pendiente de la línea utilizando la fórmula Pendiente = (CI − CN) ÷ (TN − TI). (Cuando no se puede partir del supuesto de la linealidad, el costo de la aceleración se debe determinar gráficamente por cada día que se podría abreviar la actividad.)
La ilustración 3.10 muestra los cálculos que se necesitan para obtener el costo por acelerar las actividades restantes.
No hay comentarios:
Publicar un comentario