Todo lo referido a la Administracion de operaciones y al Planeamiento y Control de la Produccion
jueves, 30 de diciembre de 2021
martes, 28 de diciembre de 2021
INNOVACIÓN - VOCABULARIO BÁSICO Parte 2
Gráfica de Gantt
Muestra gráficamente la cantidad de tiempo involucrado y la secuencia en la que se desempeñarán las actividades. Muchas veces llamada gráfica de barras.
Ruta crítica
La secuencia de las actividades de un proyecto que constituyen la cadena más larga en términos del tiempo necesario para terminarlas. Esta ruta no contiene margen de tiempo. Las técnicas utilizadas para encontrar la ruta crítica se llaman Método de la ruta crítica o MRC.
Precedente inmediato
Una actividad que debe quedar terminada justo antes de otra actividad.
Holgura de tiempo
El tiempo que se puede demorar una actividad; la diferencia entre el tiempo del inicio retrasado y el de inicio adelantado de una actividad.
Programa de inicio más próximo
El programa de un proyecto que enumera todas las actividades en razón de sus tiempos de inicio adelantado.
Programa de inicio más lejano
El programa de un proyecto que enumera todas las actividades en razón de sus tiempos de inicio retrasado. Este programa puede generar ahorros si se posponen las compras de materiales y otros costos asociados al proyecto.
Modelos de tiempo-costo
Una extensión de los modelos de la ruta crítica que considera los retos entre el tiempo requerido para terminar una actividad y su costo. Con frecuencia se llama proyecto “intensivo”.
sábado, 25 de diciembre de 2021
INNOVACIÓN - VOCABULARIO BÁSICO Parte 1
Proyecto
Una serie de trabajos relacionados que por lo habitual se dirigen hacia un producto mayor y cuyo desempeño requiere de un periodo considerable de tiempo.
Administración de proyectos
Planear, dirigir y controlar los recursos (personas, equipamiento y materiales) necesarios para cumplir con las limitaciones técnicas, de costos y de tiempo de un proyecto.
Proyecto puro
Estructura para organizar un proyecto, en cuyo caso un equipo autocontenido trabaja de tiempo completo en el proyecto.
Proyecto funcional
Estructura a la que son asignados miembros del equipo procedentes de las unidades funcionales de la organización. Los miembros del equipo siguen siendo parte de sus unidades funcionales y por lo habitual no se dedican de lleno al proyecto.
Proyecto matricial
Estructura que mezcla las estructuras del proyecto funcional y la del puro. Cada proyecto emplea a personas procedentes de distintas áreas funcionales. Un gerente de proyecto dedicado decide cuáles tareas se desempeñarán y cuándo, pero los gerentes funcionales controlan a las personas que se emplearán.
Hito del proyecto
Hecho específico de un proyecto.
Estructura de la división del trabajo
La jerarquía de tareas, subtareas y paquetes de trabajo de un proyecto.
Actividades
Pedazos de trabajo de un proyecto que consumen tiempo. La conclusión de todas las actividades de un proyecto marca el final del mismo.
martes, 21 de diciembre de 2021
INNOVACIÓN - CONCLUSIÓN
Este capítulo presenta una descripción de los fundamentos para administrar proyectos. En primer término describe, desde una óptica administrativa, la forma de organizar a las personas involucradas en un proyecto. La envergadura del proyecto sirve para defi nir la organización, la cual abarca desde el uso de un equipo dedicado hasta una estructura matricial en gran medida no dedicada. A continuación, el capítulo habla de cómo las actividades del proyecto se organizan en subproyectos utilizando la estructura de la división del trabajo. Después, se presentan los detalles técnicos para calcular el tiempo más breve que tomaría terminar un proyecto. Por último el capítulo explica cómo se pueden acortar los proyectos utilizando los conceptos de la “intensifi cación”.
jueves, 16 de diciembre de 2021
INNOVACIÓN - RASTREO DEL AVANCE
La verdadera acción empieza una vez que se ha iniciado el proyecto. El avance real diferirá del planeado originalmente, o de la línea base. El software puede contener varios planes diferentes como línea de referencia de modo que usted podrá comparar las instantáneas mensuales.
Una gráfi ca de Gantt rastreadora sobrepone el programa real sobre el plan básico de modo que las desviaciones se advierten con facilidad. Si lo prefi ere, también puede producir una hoja de cálculo para ver la misma información. Las desviaciones entre el inicio/final planeados y el inicio/fi nal recién programados también aparecen y se puede aplicar un “fi ltro corredizo” para resaltar o producir sólo aquellas tareas que están programadas para terminarse en una fecha posterior a la línea de referencia planeada.
También se puede aplicar la administración por excepción para encontrar las desviaciones entre los costos presupuestados y los reales. (Véase el recuadro de Innovación titulado “Sistemas de información para la administración de proyectos”.)
martes, 7 de diciembre de 2021
INNOVACIÓN - SISTEMAS DE INFORMACIÓN PARA LA ADMINISTRACIÓN DE PROYECTOS
El interés por las técnicas y los conceptos de la administración de proyectos ha crecido a ritmo exponencial en los pasados diez años. El resultado ha sido un incremento paralelo del software que se ofrece para tal efecto. Hoy en día, más de 100 compañías ofrecen software para la administración de proyectos. Usted puede encontrar la información más actualizada acerca del software disponible en el sito Web del Project Management Institute (www.pmi.org). Dos compañías líderes son Microsoft, con Microsoft Project, y Primavera, con Primavera Project Planner. A continuación se presenta un breve resumen de estos dos programas.
El programa Project de Microsoft cuenta con un excelente tutorial en línea, lo cual explica su abrumadora popularidad entre los gerentes de proyectos que rastrean proyectos de mediano tamaño. El paquete es compatible con Office Suite de Microsoft, el cual abre todas las comunicaciones y la capacidad de integración a Internet que ofrece Microsoft. El programa incluye características para programar, asignar y nivelar recursos, así como para controlar costos y producir gráficas e informes con calidad para presentaciones.
Por último, para administrar proyectos muy grandes o programas que tienen varios proyectos, el Primavera Project Planner suele ser el elegido. Primavera fue el primer proveedor importante en vender este tipo de software y posiblemente tiene la capacidad más sofisticada.
martes, 30 de noviembre de 2021
ADMINISTRACIÓN DE RECURSOS
Además de programar cada tarea, se deben asignar los recursos. El software moderno en seguida resalta las sobreasignaciones; es decir, situaciones en que las asignaciones exceden a los recursos.
sábado, 20 de noviembre de 2021
MODELOS DE TIEMPO-COSTO - Programación del costo mínimo (equilibrio entre tiempo-costo) Parte 3
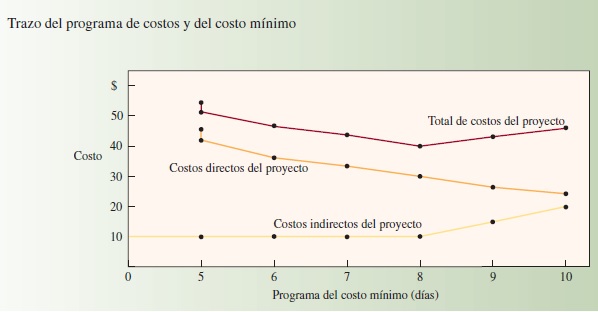
5. Trace el programa de las curvas de los costos directos del proyecto, los indirectos y el total de costos y encuentre el costo mínimo. La ilustración 3.12 presenta el costo indirecto trazado como una constante de 10 dólares por día durante ocho días, el cual incrementa 5 dólares por día a continuación. Los costos directos son trazados con base en la ilustración 3.11 y el costo total del proyecto se presenta como el total de los dos anteriores.
La suma de los costos directos y los indirectos correspondientes a cada día produce la curva del costo total del proyecto. Observará que esta curva está en su mínimo con el programa de ocho días, que cuesta 40 dólares (30 dólares de directos + 10 dólares de indirectos).
jueves, 18 de noviembre de 2021
MODELOS DE TIEMPO-COSTO - Programación del costo mínimo (equilibrio entre tiempo-costo) Parte 2
3. Calcule la ruta crítica.
En el caso de la red sencilla que se ha utilizado, este programa tomaría 10 días. La ruta crítica es A-B-D.
4. Acorte la ruta crítica al costo mínimo.
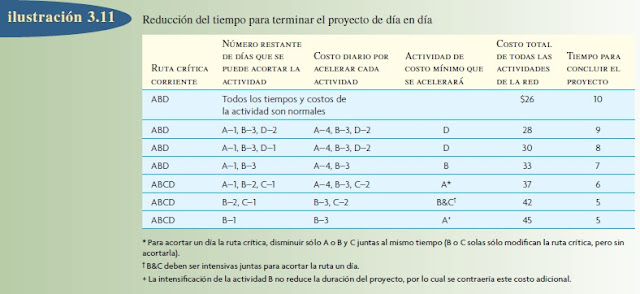
La forma más fácil de proceder es iniciar con el programa normal, encontrar la ruta crítica y acortar un día el tiempo de la ruta utilizando la actividad que tenga el costo más bajo. A continuación, recalcule y encuentre la nueva ruta crítica y disminúyala también un día. Repita este procedimiento hasta que el tiempo para terminar sea satisfactorio o hasta que no se pueda reducir más el tiempo para concluir el proyecto. La ilustración 3.11 muestra la reducción de la red de día en día.
Al principio, ir trabajando con la ilustración 3.11 podría parecer difícil. En la primera línea, todas las actividades están en sus tiempos y costos normales y a su valor más bajo. La ruta crítica es A-B-D, el costo por terminar el proyecto es $26 y el tiempo para concluirlo es de diez días.
La meta de la línea dos es acortar un día el tiempo para concluir el proyecto. Se sabe que es necesario reducir el tiempo de una o varias actividades de la ruta crítica. En la segunda columna, se advierte que es posible disminuir un día la actividad A (de dos días a uno), tres días la actividad B (de cinco días a dos) y dos días la actividad D (de tres días a uno). La siguiente columna rastrea los costos por abreviar un día cada una de las actividades. Por ejemplo, en el caso de la actividad A, el costo normal por terminarla en dos días es de 6 dólares. Se puede terminar en un día a un costo de 10 dólares, o un incremento de 4 dólares. Por lo tanto, se indica que el costo por acelerar la actividad A un día es 4 dólares. En el caso de la actividad B, el costo normal por terminarla en cinco días es de 9 dólares. Se podría terminar en dos días a un costo de 18 dólares. El costo por disminuir B tres días es de 9 dólares, o 3 dólares por día. En el caso de C, el costo normal por terminarla en tres días es de 5 dólares. Se podría terminar en un día a un costo de 9 dólares, cortarle dos días costaría 4 dólares (2 dólares por día). La opción menos costosa por abreviar el tiempo un día es acelerar la actividad D a un costo de 2 dólares. El costo total de la red sube a 28 dólares y el tiempo para concluir el proyecto se reduce a nueve días.
La siguiente iteración inicia en la línea tres, en cuyo caso la meta es bajar a ocho días el tiempo para terminar el proyecto. La ruta crítica de nueve días es A-B-D. Se podría abreviar un día la actividad A, tres días la B y un día la D (nótese que D ya se ha reducido de tres días a dos). El costo por disminuir cada actividad un día es el mismo que en la línea dos. De nueva cuenta, reducir la actividad D representa el menor costo. El resultado de acortar la actividad D de dos días a uno es que el costo total de todas las actividades de la red ascienda a 30 dólares y que el tiempo para concluir el proyecto se reduzca a ocho días.
La línea cuatro es similar a la tres, pero ahora sólo A y B están en la ruta crítica y se pueden disminuir. Se acorta B y el costo sube 3 dólares (a 33 dólares) y el tiempo para concluir el proyecto se reduce a siete días.
En la línea cinco (de hecho la quinta iteración para resolver el problema), las cuatro actividades A, B, C y D son críticas. La D no se puede disminuir, por lo cual las opciones son las actividades A, B y C. Nótese que B y C son paralelas, por lo cual no sirve de nada disminuir B sin disminuir C. Las opciones son acortar sólo A, a un costo de 4 dólares, o B y C juntas, a un costo de 5 dólares (3 dólares de B y 2 dólares de C), por lo cual en esta iteración se reduce A.
En la línea seis, se toma la opción de B y C que se considera en la línea cinco. Por último, en la línea siete, la única opción es acortar la actividad B. Dado que B y C son paralelas y que no es posible acortar C, no tiene sentido reducir sólo la B. Aquí, ya no se puede disminuir más el tiempo para terminar el proyecto.
martes, 9 de noviembre de 2021
MODELOS DE TIEMPO-COSTO - Programación del costo mínimo (equilibrio entre tiempo-costo) Parte 1
El supuesto básico del programa de costos mínimos es que existe una relación entre el tiempo para terminar una actividad y el costo de un proyecto. Por un lado, acelerar una actividad cuesta dinero y, por el otro, sostener (o prolongar) el proyecto también cuesta dinero. Los costos asociados a acelerar las actividades se llaman costos directos de las actividades y se suman al costo directo del proyecto. Algunos pueden estar relacionados con el trabajo, como las horas extra, la contratación de más trabajadores y el traslado de trabajadores procedentes de otros trabajos, otros están relacionados con los recursos, como la compra o el arrendamiento de equipamiento adicional o más eficiente y el uso de instalaciones adicionales de apoyo.
Los costos asociados a sostener el proyecto se llaman costos indirectos del proyecto: gastos fijos, instalaciones y costos de oportunidad de los recursos y, en ciertas situaciones contractuales, los costos de penalización o los pagos de incentivos que se pierden. Dado que los costos directos de las actividades y los costos indirectos del proyecto son costos contrarios que dependen del tiempo, el problema de su programación depende en esencia de encontrar la duración del proyecto que minimiza su suma o, en otras palabras, de encontrar el punto óptimo en un equilibrio de tiempo-costo.
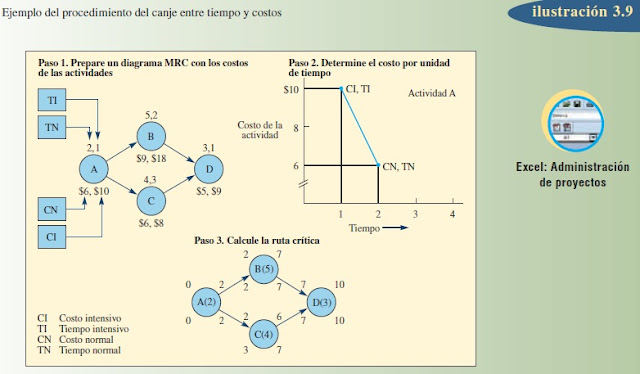
El procedimiento para encontrar este punto consiste en los siguientes cinco pasos y se explica utilizando la red simple de cuatro actividades que presenta la ilustración 3.9. Suponga que los costos indirectos permanecen constantes durante ocho días y que, a continuación, incrementan a un ritmo de 5 dólares por día.
1. Prepare un diagrama de red tipo MRC.
Para cada actividad, este diagrama debe enumerar:
a) El costo normal (CN): los costos más bajos esperados para la actividad. (Se trata de las cifras de costos más bajas que se presentan bajo cada nodo en la ilustración 3.9.)
b) El tiempo normal (TN): el tiempo asociado a cada costo normal.
c) El tiempo intensivo (TI): el tiempo más breve posible de cada actividad.
d) El costo intensivo (CI): el costo asociado a cada tiempo intensivo.
2. Determine el costo por unidad de tiempo (suponga días) para acelerar cada actividad.
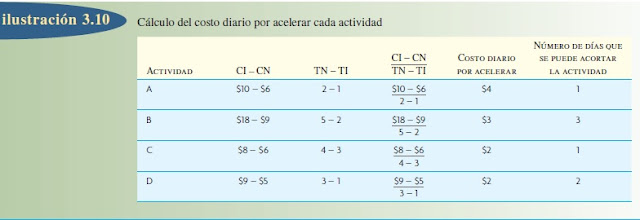
La relación entre el tiempo y el costo de la actividad se puede representar gráficamente trazando las coordenadas CI y TI y conectándolas con las coordenadas CN y TN mediante una línea cóncava, convexa o recta, o de alguna otra forma, dependiendo de la estructura real del costo del desempeño de la actividad, como en la ilustración 3.9. Para la actividad A, se supone una relación lineal entre el tiempo y el costo. Este supuesto es común en la práctica y sirve para derivar el costo por día por acelerar las cosas porque este valor se puede encontrar directamente tomando la pendiente de la línea utilizando la fórmula Pendiente = (CI − CN) ÷ (TN − TI). (Cuando no se puede partir del supuesto de la linealidad, el costo de la aceleración se debe determinar gráficamente por cada día que se podría abreviar la actividad.)
La ilustración 3.10 muestra los cálculos que se necesitan para obtener el costo por acelerar las actividades restantes.
viernes, 5 de noviembre de 2021
MODELOS DE TIEMPO-COSTO
En la práctica, los gerentes de proyectos se interesan tanto por el costo para terminar un proyecto, como por el tiempo para concluirlo. Por ello, han creado modelos de tiempo-costo. Estos modelos, que son extensiones del método básico de la ruta crítica, tratan de elaborar un programa de costos mínimos para el proyecto entero y de controlar los egresos durante el proyecto.
domingo, 24 de octubre de 2021
EJEMPLO 3.2: Tres estimados de tiempo - SOLUCIÓN Parte 2
Dado que la red tiene dos rutas críticas, hay que decidir cuáles variaciones se deben emplear para llegar a la probabilidad de cumplir con la fecha de conclusión del proyecto. Un enfoque conservador dicta utilizar la ruta con la variación total más grande para concentrar la atención de la gerencia en las actividades que tienen mayor probabilidad de exhibir grandes variaciones. Así, las variaciones asociadas a las actividades A, C, F y G se usarían para encontrar la probabilidad de la conclusión. Por lo tanto
Suponga que la gerencia quiere la probabilidad de finalizar el proyecto en 35 semanas, en tal caso D es 35. Se encontró que el tiempo esperado para la conclusión era 38. Sustituyendo en la ecuación Z y resolviéndola se tiene
En el apéndice E se observa que un valor de Z de −0.87 da una probabilidad de 0.1922, lo cual significa que el gerente del proyecto sólo tiene una probabilidad de 19% de concluir el proyecto en 35 semanas. Nótese que esta probabilidad es la de realmente concluir con la ruta crítica A-C-F-G. Dado que existe otra ruta crítica y otras rutas que se podrían volver críticas, la probabilidad de terminar el proyecto en 35 semanas de hecho es menor a 0.19.
lunes, 18 de octubre de 2021
ANÁLISIS DE PROBABILIDADES
El enfoque de los tres estimados de tiempo permite considerar la probabilidad de que un proyecto quede terminado dentro de una cantidad de tiempo dada. El supuesto que sirve de base para calcular esta probabilidad es que los tiempos de duración de las actividades son variables aleatorias independientes. De ser así, se puede utilizar el teorema del límite central para encontrar la media y la varianza de la secuencia de actividades que constituyen la ruta crítica. El teorema del límite central dice que la suma de un grupo de variables aleatorias independientes, distribuidas de forma idéntica, se acerca a una distribución normal a medida que el número de variables aleatorias se incrementa. En el caso de problemas de administración de proyectos, las variables aleatorias son los tiempos reales de las actividades del proyecto. (Recuerde que se supone que el tiempo para cada actividad es independiente de otras actividades, y que sigue una distribución estadística beta.) Para ello, el tiempo esperado para terminar las actividades de la ruta crítica es la suma de los tiempos de las actividades.
Asimismo, dado el supuesto de la independencia de los tiempos de las actividades, la suma de las varianzas de las actividades a lo largo de la ruta crítica es la varianza del tiempo esperado para concluir la ruta. Recuerde que la desviación estándar es igual a la raíz cuadrada de la varianza.
Para determinar la probabilidad real de concluir las actividades de la ruta crítica dentro de una cantidad dada de tiempo, es necesario encontrar dónde se ubica el punto dentro de la distribución de probabilidad.
El apéndice E presenta las áreas de la distribución normal estándar acumulada para diferentes valores de Z. Ésta mide el número de desviaciones estándar, hacia la derecha o la izquierda de cero, en la distribución. Con referencia al apéndice E, los valores G(z) son el área bajo la curva que representan la distribución. Los valores corresponden a la probabilidad acumulada asociada a cada valor de Z. Por ejemplo, el primer valor de la tabla, −4.00 tiene un G(z) igual a 0.00003. Esto significa que la probabilidad asociada a un valor Z de −4.0 es tan sólo 0.003%. Por otro lado, un valor Z de 1.50 tiene un G(z) igual a 0.93319 o 93.319%. Los valores de Z se calculan con la ecuación (3.3) presentada en el paso 7b de la solución del ejemplo “Tres estimados de tiempo”. Estas probabilidades acumuladas también se pueden obtener con la función DISTR.NORM.ESTAND (Z) incluida en Excel de Microsoft.
martes, 12 de octubre de 2021
EJEMPLO 3.2: Tres estimados de tiempo - SOLUCIÓN Parte 1
EJEMPLO 3.2: Tres estimados de tiempo
Se utiliza la misma información que en el ejemplo 3.1, con la salvedad de que las actividades tienen tres estimados de tiempo.
SOLUCIÓN
1. Identifique cada una de las actividades que se deben realizar en el proyecto.
2. Determine la secuencia de las actividades y construya una red que refleje las relaciones de precedencia.
3. Los tres estimados del tiempo de una actividad son:
a = Tiempo optimista: el periodo mínimo razonable en el cual es posible terminar la actividad. (Sólo existe una probabilidad mínima [por lo general se supone que es de 1% de que la actividad se pueda terminar en menos tiempo.)
m = Tiempo más probable: el supuesto más próximo al tiempo que se requerirá. Dado que m sería considerado el tiempo más probable en presentarse, también es el modo de la distribución beta que se explica en el paso 4.
b = Tiempo pesimista: el periodo máximo razonable en el cual es posible terminar la actividad. (Sólo existe una pequeña probabilidad [por lo general se supone que es de 1%] de que tomaría más tiempo.) Por lo general, esta información se obtiene de las personas que habrán de desempeñar la actividad.
4. Calcule el tiempo esperado (TE) para cada actividad. La fórmula del cálculo es
5. Determine la ruta crítica. Con los tiempos esperados, la ruta crítica se calcula de la misma manera que en el caso de un solo tiempo.
6. Calcule las varianzas (σ 2) de los tiempos de la actividad. En específico, se trata de la varianza, σ 2, asociada a cada TE y se calcula así:
a) Sume los valores de las variaciones asociadas a cada actividad de la ruta crítica.
b) Sustituye esta cifra, así como la fecha final del proyecto y el tiempo de conclusión esperado del proyecto en la fórmula Z de transformación. La fórmula es la siguiente:
c) Calcule el valor de Z, que es el número de las desviaciones estándar (de una distribución normal estándar) de la fecha de vencimiento del proyecto con relación al tiempo esperado para su conclusión.
d) Utilizando el valor de Z, encuentre la probabilidad de cumplir con la fecha fi nal del proyecto (utilizando una tabla de probabilidades normales como la del apéndice E). El tiempo esperado para la conclusión es el tiempo de inicio más la suma de los tiempos de las actividades de la ruta crítica.
Siguiendo los pasos que se acaban de describir, se creó la ilustración 3.7, la cual presenta los tiempos esperados y las varianzas. La red del proyecto fue creada de la misma manera que antes. La única diferencia es que los tiempos de las actividades son promedios ponderados. Hay que determinar la ruta crítica como antes, utilizando estos valores como si fueran simples números. La diferencia entre los estimados de un tiempo y de tres tiempos (optimista, más probable y pesimista) radica en el cálculo de las probabilidades de terminación.
La ilustración 3.8 muestra la red y la ruta crítica.
domingo, 10 de octubre de 2021
MRC CON TRES ESTIMADOS DE TIEMPO PARA LAS ACTIVIDADES
Cuando un solo estimado del tiempo requerido para terminar una actividad no es confiable, el procedimiento más aconsejable es utilizar tres estimados. Estos tres estimados no sólo permiten estimar el tiempo de la actividad, sino que también permiten obtener un estimado de la probabilidad del tiempo para la conclusión de la red entera. Brevemente, el procedimiento es el siguiente: el tiempo estimado de la actividad se calcula utilizando un promedio ponderado del estimado mínimo de tiempo, el máximo y el más probable. El tiempo esperado para la conclusión de la red se calcula utilizando el procedimiento antes descrito. Así, utilizando los estimados de la variabilidad de las actividades de la ruta crítica es posible estimar la probabilidad de terminar el proyecto en un tiempo determinado. (Nótese que los cálculos de probabilidad son una característica distintiva del enfoque clásico de la PERT.)
sábado, 9 de octubre de 2021
EJEMPLO 3.1: Método de la ruta crítica - Un programa de inicio más lejano
Un programa de inicio más lejano enumera las actividades que pueden iniciar lo más tarde posible, sin retrasar la fecha del fi nal del proyecto. Un motivo para utilizar un programa de inicio retrasado es que se realizan ahorros cuando se posponen las compras de materiales, el uso de trabajo y otros costos hasta el momento en que se necesitan. La ilustración 3.6 muestra estos cálculos. En ellos se puede ver que la única actividad que tiene margen de tiempo es la E. No cabe duda que será bastante difícil terminar este proyecto a tiempo.
viernes, 8 de octubre de 2021
EJEMPLO 3.1: Método de la ruta crítica - Programas de inicio más próximo e inicio más lejano
Un programa de inicio más próximo enumera todas las actividades en razón de sus tiempos de inicio más próximo. En el caso de actividades que no están en la ruta crítica existe un margen de tiempo entre el final de cada actividad y el inicio de la siguiente. El programa de inicio más próximo concluye el proyecto y todas sus actividades lo más pronto posible.
martes, 5 de octubre de 2021
EJEMPLO 3.1: Método de la ruta crítica - Solución
El primer encargo del equipo del proyecto es elaborar una gráfica de la red del proyecto y estimar la probabilidad de terminar el prototipo de la computadora en un plazo de 35 semanas. En seguida aparecen los pasos para elaborar la red.
1. Identifique las actividades.
El equipo del proyecto decide que las actividades siguientes son los elementos principales del proyecto: diseño de la computadora, construcción del prototipo, pruebas del prototipo, especificación de los métodos (resumidos en un informe), estudios de evaluación del equipo automático de montaje, un informe del estudio del equipo de montaje y un informe final que resuma todos los aspectos del diseño, el equipo y los métodos.
2. Construya la red y la secuencia de las actividades.
Con base en una charla con el personal, el gerente del proyecto prepara la tabla de precedentes y la secuencia de la red que muestra la ilustración 3.5. Cuando construya una red, asegúrese de que las actividades están en el orden adecuado y que conserva la lógica de sus relaciones. Por ejemplo, sería ilógico tener una situación en la cual el hecho A precede al hecho B, el B precede al C y el C precede al A.
3. Determine la ruta crítica.
La ruta crítica es la secuencia más larga de actividades conectadas a lo largo de la red y se defi ne como la ruta sin margen de tiempo alguno. Esta red tiene cuatro rutas diferentes: A-C-F-G, A-C-E-G, A-B-D-F-G y A–B-D-E-G. La longitud de estas rutas es de 38, 35, 38 y 35 semanas.
Advierta que este proyecto tiene dos rutas críticas diferentes, lo cual indicaría que la administración de este proyecto puede ser bastante difícil. El cálculo de los programas de inicios más próximos y más lejanos proporciona más información respecto a la posible dificultad para concluir el proyecto a tiempo. •
martes, 28 de septiembre de 2021
EJEMPLO 3.1: Método de la ruta crítica
Muchas compañías que han tratado de entrar en el mercado de las computadoras notebook han fracasado. Suponga que su empresa piensa que existe una enorme demanda en ese mercado porque los productos existentes no han sido diseñados correctamente. Son demasiado pesados, demasiado grandes o demasiado pequeños como para tener teclados de tamaño estándar. La computadora que usted desea será lo bastante pequeña como para cargarla en el bolsillo de una chaqueta en caso necesario. El tamaño ideal no pasará de 5 × 91/2 × 1 pulgadas, con un teclado plegable. No pesará más de 15 onzas y tendrá pantalla de cristal líquido (LCD), un micro drive de disco y una conexión inalámbrica. Así, le resultará atractiva a los empresarios que viajan, pero podría tener un mercado mucho más amplio, inclusive entre los estudiantes. Su precio estará en la banda de 175-200 dólares.
Así pues, el proyecto consiste en diseñar, desarrollar y producir un prototipo de esta pequeña computadora.
Dados los veloces cambios de la industria de las computadoras, es fundamental llegar al mercado con un producto de este tipo en menos de un año. Por lo tanto, el equipo del proyecto cuenta con unos ocho meses (35 semanas) para producir el prototipo.
viernes, 24 de septiembre de 2021
MÉTODO DE LA RUTA CRÍTICA (MRC) - Determine el inicio/final más próximo o el inicio/final más lejano del programa.
A efecto de programar el proyecto, encuentre cuándo debe iniciar cada actividad y cuándo debe quedar terminada. En el caso de algunas actividades de un proyecto puede haber cierto margen para el momento en que las actividades pueden iniciar o terminar y se llama holgura de tiempo de una actividad. Tomando cada actividad del proyecto, se calculan cuatro puntos de tiempo: el inicio más próximo, el final más próximo, el inicio más lejano y el final más lejano. El inicio más próximo y el final más próximo se refieren a lo más pronto que puede iniciar o terminar una actividad. Por otro lado, el inicio más lejano y el final más lejano se refieren a lo más tarde que puede iniciar o terminar una actividad. La diferencia entre el tiempo del inicio más lejano y el inicio más próximo es la holgura de tiempo. Para que todo lo anterior quede claro, se colocan estos números en lugares especiales en torno a los nodos que representan cada una de las actividades de la red del diagrama, como se muestra al lado.
Para calcular los números, empiece al principio de la red y avance hasta llegar al final, calculando los números correspondientes al inicio más próximo y el final más próximo. Empiece a contar en el periodo actual, llamado periodo 0. La actividad A tiene un inicio más próximo de 0 y un final más próximo de 1. El inicio más próximo de la actividad B es el final más próximo de A, o 1. Asimismo, el inicio más próximo de C es 1. El final más próximo de B es 3 y el final más próximo de C es 2. Ahora considere la actividad D. Ésta no puede iniciar hasta que B y C estén terminadas. Dado que B no puede quedar terminada hasta 3, D sólo podrá iniciar en ese tiempo.
Por lo tanto, el inicio más próximo de D es 3 y su final más próximo es 4. Ahora el diagrama luce así:
miércoles, 22 de septiembre de 2021
MÉTODO DE LA RUTA CRÍTICA (MRC) - Determine la ruta crítica.
Considere cada secuencia de actividades que se ejecuta de principio a fin del proyecto. En el proyecto sencillo hay dos rutas: A-B-D y A-C-D. La ruta crítica es Precedentes inmediatos aquella donde la suma de los tiempos de las actividades es la más larga. A-B-D tiene una duración de cuatro semanas y A-C-D tiene una de tres semanas. Por lo tanto, la ruta crítica es A-B-D. Si alguna actividad dentro de la ruta crítica se demora, entonces el proyecto entero se retrasará.
miércoles, 15 de septiembre de 2021
MÉTODO DE LA RUTA CRÍTICA (MRC) Parte 2
Se trata de un proyecto sencillo, pero servirá para demostrar el enfoque. A continuación se presentan los pasos correspondientes.
1. Identifique cada una de las actividades que se de sempeñarán en el proyecto y estime el tiempo que tomará concluir cada actividad. Esto es sencillo, dada la información que ha proporcionado el profesor. Las actividades se identifican como A(1), B(2), C(1) y D(1). El número se refiere a la duración esperada de la actividad.
2. Determine la secuencia requerida de las actividades y construya una red que refleje las relaciones precedentes. Un camino fácil para hacerlo es identificar primero los precedentes inmediatos asociados a una actividad. Los precedentes inmediatos se refieren a las actividades que se deben terminar justo antes de otra actividad. Es preciso terminar la actividad A para que puedan empezar la actividad B y la C. Es necesario terminar la B y la C para que pueda empezar la D. La tabla siguiente representa lo que se sabe hasta aquí.
jueves, 26 de agosto de 2021
MÉTODO DE LA RUTA CRÍTICA (MRC) Parte 1
Se trata de un procedimiento para programar un proyecto. En este caso, se utiliza un único estimado de tiempo, porque se supone que se conocen los tiempos de la actividad. Se programará un proyecto muy sencillo para demostrar el enfoque básico.
Piense que le han dejado una tarea de grupo que requiere decidir si se debe invertir en una compañía o no. Su profesor ha sugerido que hagan el análisis siguiendo cuatro pasos:
a) Escoger una compañía.
b) Conseguir el informe anual de esa compañía y hacer un análisis de proporciones.
c) Reunir datos técnicos del precio de las acciones y crear gráficas.
d) Revisar individualmente los datos y tomar una decisión en equipo respecto a comprar las acciones o no.
Las cuatro personas de su grupo deciden que el proyecto se puede dividir en las cuatro actividades que ha sugerido el profesor. Deciden que todos los miembros del equipo deben participar en la selección de la compañía y que esta actividad debe quedar terminada en una semana. Todos se reunirán al término de la misma para decidir cuál compañía considerará el grupo. En esa junta, el grupo se dividirá: dos personas serán encargadas del informe anual y el análisis de proporciones, y las otras dos reunirán los datos técnicos y crearán las gráfi cas. Su grupo estima que conseguir el informe anual y hacer el análisis de proporciones les tomará dos semanas y que reunir los datos del precio de las acciones y generar las gráficas les tomará una semana. Todos consideran que los dos grupos pueden trabajar de forma independiente.
Por último, acuerdan que el equipo se reunirá para tomar la decisión de compra. Antes de reunirse, quieren tomar una semana para que cada miembro del equipo pueda revisar todos los datos.
jueves, 19 de agosto de 2021
MODELOS DE PLANEACIÓN DE REDES
sábado, 14 de agosto de 2021
GRÁFICAS DE CONTROL DEL PROYECTO Parte 4
La ilustración 3.4E es una gráfi ca de hitos. Los tres hitos marcan puntos específi cos del proyecto en los cuales se pueden hacer revisiones para comprobar si el proyecto avanza puntualmente y dónde se debería encontrar. El mejor lugar para colocar los hitos es en el punto donde termina una actividad mayor.
En esta ilustración, las actividades mayores terminadas fueron “órdenes de compra giradas”, “facturas recibidas” y “materiales recibidos”.
Se pueden emplear otros informes estándar para tener un presentación más detallada de la comparación de los costos con el avance (como el informe de situación de la relación de costos-RSRC) o informes que sientan las bases para pagos parciales (como el informe de valor devengado).
martes, 10 de agosto de 2021
GRÁFICAS DE CONTROL DEL PROYECTO Parte 3
lunes, 2 de agosto de 2021
GRÁFICAS DE CONTROL DEL PROYECTO Parte 2
La ilustración 3.4C muestra el porcentaje de horas laborables del proyecto que corresponden a las áreas de producción, fi nanzas y otras más. Estas horas laborables están relacionadas con la proporción del costo total del trabajo del proyecto. Por ejemplo, 50% de las horas laborables del proyecto corresponden a producción, pero sólo 40% del total de los dólares de trabajo cargados han sido asignados a este 50 por ciento.
miércoles, 7 de julio de 2021
GRÁFICAS DE CONTROL DEL PROYECTO Parte 1
El Departamento de Defensa de Estados Unidos (uno de los primeros en usar extensamente la administración de proyectos) ha publicado una serie de formas estándar que resultan muy útiles. Muchas de ellas han sido utilizadas directamente o han sido modificadas por empresas que emplean la administración de proyectos. Existen programas de computadora que generan con rapidez las gráficas que se describirán en esta sección. Estas gráficas son muy útiles porque su presentación visual es fácil de comprender. La ilustración 3.4 presenta una muestra de las gráficas disponibles.
La ilustración 3.4A es una muestra de una gráfica de Gantt, a veces llamada gráfica de barras, que muestra tanto la cantidad de tiempo involucrada como la secuencia en que se desempeñarían las actividades.
La gráfica debe su nombre a Henry L. Gantt, quien mereció un reconocimiento presidencial por haber aplicado este tipo de gráfica a la construcción de barcos durante la Primera Guerra Mundial. En el ejemplo de la ilustración 3.4A, “las adquisiciones con mucho tiempo” y los “programas de producción” son actividades independientes y se pueden dar de forma simultánea. Todas las demás actividades se deben desempeñar en secuencia, de arriba hacia abajo. Las gráfi cas de la ilustración 3.4B representan los montos de dinero gastados en mano de obra, materiales y gastos fi jos. Su valor radica en su claridad para identificar las fuentes y los montos de los costos.
sábado, 3 de julio de 2021
ESTRUCTURACIÓN DE LOS PROYECTOS - PROYECTO MATRICIAL - ESTRUCTURA DE LA DIVISIÓN DEL TRABAJO Parte 2
La ilustración 3.3 muestra la EDT para el proyecto de un escáner óptico. La EDT es importante para organizar un proyecto porque divide el proyecto en partes manejables. El número de niveles variará dependiendo del proyecto. La cantidad de detalles o de niveles que se emplearán dependerá de lo siguiente:
• La medida en que se pueda encargar a un individuo o una organización el paquete de trabajo y adjudicarle la responsabilidad de que el paquete quede terminado.
• La medida en que se reúnan datos del presupuesto y los costos durante el proyecto.
No existe una EDT que sea la correcta para un proyecto y los equipos de dos proyectos diferentes podrían desarrollar diferentes EDT para el mismo proyecto. Algunos expertos dicen que la administración de proyectos es más un arte que una ciencia, porque existen muchos caminos distintos para abordar un proyecto. La posibilidad de encontrar la manera correcta de organizar un proyecto depende de la experiencia que se tenga con una tarea particular.
Las actividades se defi nen dentro del contexto de la estructura de división del trabajo y son partes del trabajo que consumen tiempo. Las actividades no requieren necesariamente que las personas hagan un esfuerzo, aun cuando es frecuente que sí lo requieran. Por ejemplo, esperar a que la pintura se seque podría ser una actividad dentro de un proyecto. Las actividades se identifi can como parte de la EDT.
Según el proyecto de muestra de la ilustración 3.3, las actividades incluirían el diseño y la fabricación del telescopio (1.1.1), la interfaz del telescopio/simulador óptico (1.1.2) y el registro de datos (1.2.4). Las actividades deben estar defi nidas de modo que cuando todas ellas queden terminadas, el proyecto llegará a su fi n.
martes, 25 de mayo de 2021
ESTRUCTURACIÓN DE LOS PROYECTOS - PROYECTO MATRICIAL - ESTRUCTURA DE LA DIVISIÓN DEL TRABAJO Parte 1
Un proyecto inicia como un enunciado de trabajo (ET). Este enunciado puede ser una descripción por escrito de los objetivos que se alcanzarán, con una breve reseña del trabajo que se desempeñará y un calendario propuesto que plantea la fecha de inicio y la de conclusión. También puede contener medidas del desempeño en términos de presupuesto y pasos terminados (hitos) y los informes que se presentarán por escrito.
Una tarea representa una subdivisión más de un proyecto. Por lo general sólo dura algunos meses y es desempeñada por un grupo u organización. En caso necesario, se puede utilizar una subtarea para subdividir el proyecto en partes que tengan mayor sentido.
Un paquete de trabajos es un grupo de actividades combinadas que serán asignadas a una sola unidad organizacional. El paquete sigue adoptando el formato de toda administración de proyectos y presenta una descripción de lo que se hará, cuándo se iniciará y concluirá, el presupuesto, las medidas del desempeño y los hechos específi cos que deben estar terminados en puntos determinados de tiempo.
Estos hechos específi cos se llaman hitos del proyecto. Algunos hitos típicos serían terminar el diseño, producir un prototipo, terminar las pruebas del prototipo y autorizar una corrida piloto.
La estructura de la división del trabajo (EDT) defi ne la jerarquía de las tareas, las subtareas y los paquetes de trabajo del proyecto. Cuando se terminan uno o varios paquetes de trabajo se termina una subtarea, cuando se terminan una o varias subtareas se termina una tarea y, por último, es necesario terminar todas las tareas para que el proyecto quede concluido. La ilustración 3.2 presenta esta estructura.
domingo, 9 de mayo de 2021
ESTRUCTURACIÓN DE LOS PROYECTOS - PROYECTO MATRICIAL - Ventajas y Desventajas
VENTAJAS
• Se fortalece la comunicación entre las divisiones funcionales.
• El gerente de un proyecto es el encargado de que el proyecto llegue a buen término.
• La duplicación de recursos se reduce al mínimo.
• Los miembros del equipo tienen un “hogar” funcional una vez que se ha terminado el proyecto, por lo cual están menos preocupados por su existencia después del proyecto que si estuvieran dentro de un proyecto puro.
• Se siguen las políticas de la organización matriz, lo cual incrementa el apoyo que se brinda al proyecto.
DESVENTAJAS
• Hay dos jefes. Con frecuencia se hace más caso al gerente funcional que al del proyecto. Al final de cuentas, ¿quién está en posición de prometerle u otorgarle un aumento de sueldo?
• Está condenado al fracaso a no ser que el GP tenga sólidas habilidades para la negociación.
• La suboptimización representa un peligro, dado que los GP acaparan recursos • para sus proyectos, afectando con ello otros proyectos.
Advierta que sea cual fuere la forma de organización básica de las tres mencionadas que se utilice, el gerente del proyecto es el principal punto de contacto con el cliente. La comunicación y la fl exibilidad se refuerzan porque una persona es la responsable de que el proyecto llegue a buen término.
sábado, 8 de mayo de 2021
ESTRUCTURACIÓN DE LOS PROYECTOS - PROYECTO MATRICIAL
La forma clásica de organización especializada, o “el proyecto matricial”, busca mezclar las propiedades de la estructura del proyecto puro y la del funcional. Cada proyecto utiliza a personas de distintas áreas funcionales. El gerente del proyecto (GP) decide cuáles tareas se desempeñarán y cuándo, pero los gerentes funcionales controlan cuáles personas y tecnologías se emplearán. Si se opta por la forma de matriz, distintos proyectos (hileras de la matriz) toman recursos a préstamo de las áreas funcionales (columnas). A continuación, la alta gerencia debe decidir si se utilizará una matriz de forma débil, equilibrada o fuerte. Esto determina si los gerentes del proyecto tendrán poca, igual o más autoridad que los gerentes funcionales con los cuales negocian para obtener recursos.
viernes, 7 de mayo de 2021
ESTRUCTURACIÓN DE LOS PROYECTOS - PROYECTO FUNCIONAL
En el otro extremo del espectro de la organización de proyectos está el proyecto funcional, el cual aloja el proyecto dentro de una división funcional.
VENTAJAS
• Un miembro de un equipo puede trabajar en varios proyectos.
• La experiencia técnica se conserva dentro del área funcional a pesar de que los individuos abandonen el proyecto o la organización.
• El proyecto. Los especialistas en las funciones pueden avanzar en un plano vertical.
• Una masa crítica de expertos especializados en un área funcional crea soluciones sinérgicas para los problemas técnicos del proyecto.
DESVENTAJAS
• Algunos de los aspectos del proyecto que no están relacionados directamente con el área funcional no salen bien librados.
• La motivación de los miembros del equipo suele ser poca.
• Las necesidades del cliente ocupan un segundo lugar y se responde a ellas con lentitud.
miércoles, 5 de mayo de 2021
INNOVACIÓN EL TELÉFONO CELULAR RAZR DE MOTOROLA
El nuevo RAZR de Motorola fue incubado y “empollado” en cubículos carentes de color en Libertyville, suburbio del norte de Chicago. Fue un proyecto de madriguera con un equipo estrechamente unido, que infringió, una y otra vez, las reglas de la propia compañía para el desarrollo de nuevos productos.
Los miembros manejaron el proyecto con total sigilo, sin mencionarlo siquiera a sus colegas. Utilizaron materiales y técnicas que Motorola no había empleado nunca antes. Después de acaloradas batallas internas, sacaron modelos aceptados de cómo debería lucir y sentirse un teléfono móvil. En pocas palabras, el equipo que creó el RAZR rompió el molde y, al hacerlo, rejuveneció a la compañía.
El diseño del aspecto, el manejo y también la configuración interna de un teléfono requiere de un equipo de especialistas.
En el caso del RAZR, fueron unas 20 personas. El equipo entero se reunía diariamente a las 4 de la tarde, en una sala de conferencias en Libertyville, para repasar los avances del día anterior, al mismo tiempo que recorrían una lista de comprobación de los componentes: antena, altavoz, teclado, cámara, pantalla, fuente de luz, batería, puerto de carga, etc. La junta estaba programada para una hora, pero con frecuencia terminaba después de las 7 de la tarde. El proyecto de la “almeja delgada” se convirtió en un puesto rebelde ubicado en el exterior.
El dinero no era problema alguno ni tampoco una limitante, pero la velocidad y el sigilo sí lo eran. El equipo tenía prohibido tomar fotos digitales del proyecto para que no se diseminara nada inadvertidamente por el e-mail. Los modelos del teléfono sólo podían salir del predio cuando un miembro del equipo los llevaba consigo o los acompañaba.
Dos innovaciones fundamentales permitieron al equipo hacer un salto cuántico en la delgadez, una de las características fundamentales del diseño que se pretendía lograr. La primera consistió en colocar la antena en la bocina del teléfono, y no en la parte superior. Esto no se había hecho en un teléfono celular y fue todo un reto técnico. La segunda tormenta de ideas giró en torno a reordenar la parte interior del teléfono, principalmente colocando la batería junto al tablero de circuitos (o la computadora interna), en lugar de hacerlo debajo de él. Sin embargo, esta solución creó un nuevo problema: el ancho. Los expertos en “factores humanos” de Motorola habían llegado a la conclusión de que un teléfono de más de 49 milímetros de ancho no cabía bien en la mano de una persona. El diseño de “lado con lado” producía un teléfono de 53 milímetros de ancho.
Sin embargo, el equipo del RAZR no aceptó la investigación de la compañía como si fuera la Biblia. El equipo fabricó su propio modelo para saber cómo se sentía un teléfono de 53 milímetros y, al fi nal de cuentas, sus miembros decidieron por su cuenta que la compañía estaba equivocada y que los cuatro milímetros extra eran aceptables.
La compañía vendió su RAZR número 50 millones en junio de 2006. Este año Motorola venderá más RAZR que los iPods que venderá Apple. Se solicitó a varios actores del equipo de desarrollo del RAZR que asistieran a una junta de ejecutivos de alto nivel en la ofi cina central de la compañía. No se les dijo para qué. Después, conforme los miembros fueron entrando, los jefes de Motorola que les esperaban se pusieron de pie para aplaudir en una sonora ovación. También se informó a los miembros del equipo que serían premiados con un considerable bono de opciones de acciones.
lunes, 3 de mayo de 2021
ESTRUCTURACIÓN DE LOS PROYECTOS - PROYECTO PURO
Tom Peters ha pronosticado que la mayor parte del trabajo en el mundo será “cerebral” y que se desempeñará en redes semipermanentes de equipos pequeños orientados a proyectos, cada uno con un centro autónomo de oportunidades emprendedoras, donde la necesidad de velocidad y fl exibilidad son una sentencia de muerte para las estructuras administrativas jerárquicas con las que crecimos, al igual que nuestros antepasados. Por lo tanto, de las tres estructuras organizacionales básicas para los proyectos, Peters prefi ere el proyecto puro (llamado trabajo de madriguera), en cuyo caso un equipo autocontenido trabaja de tiempo completo en el proyecto.
VENTAJAS
El gerente del proyecto t • iene plena autoridad sobre el mismo.
• Los miembros del equipo dependen de un jefe. No tienen que preocuparse por dividir su lealtad con el gerente de un área funcional.
• Las líneas de comunicación son más cortas. Las decisiones se toman con rapidez.
• El orgullo, la motivación y el compromiso del equipo son enormes.
DESVENTAJAS
• Duplicación de recursos. El equipamiento y las personas no son compartidos entre proyectos.
• Las metas y las políticas de la organización son ignoradas, dado que los miembros del equipo muchas veces están lejos, en términos físicos y psicológicos, de la ofi cina matriz.
• La organización se rezaga en su conocimiento de la nueva tecnología porque las divisiones funcionales se debilitan.
miércoles, 28 de abril de 2021
ESTRUCTURACIÓN DE LOS PROYECTOS
Antes de que inicie un proyecto, la alta gerencia debe decidir cuál de tres estructuras organizacionales utilizará para ligar el proyecto a la empresa matriz: un proyecto puro, un proyecto funcional o un proyecto matricial. A continuación se explican las ventajas y las desventajas de estas tres formas básicas.
lunes, 26 de abril de 2021
¿QUÉ QUIERE DECIR ADMINISTRACIÓN DE PROYECTOS?
Cabe defi nir un proyecto como una serie de trabajos relacionados que, por lo habitual, se dirigen hacia un producto mayor y cuyo desempeño requiere de un periodo considerable. La administración de proyectos se puede defi nir como la planeación, la dirección y el control de recursos (personas, equipamiento y materiales) para poder sujetarse a las limitantes técnicas, de costo y de tiempo del proyecto.
Con frecuencia se piensa que los proyectos sólo ocurren una vez, pero la realidad es que muchos de ellos se repiten o trasladan a otros contextos o productos. El resultado será otro producto del proyecto. El contratista que construye casas o la empresa que fabrica productos en poco volumen, como supercomputadoras, locomotoras o aceleradores lineales, de hecho puede pensar que se trata de proyectos.
domingo, 25 de abril de 2021
EL IPOD DE APPLE TIENE SU PROPIO EQUIPO DE DESARROLLO DEL PRODUCTO Parte 3
En este capítulo sólo se revisa parcialmente la presentación al tema de la administración de proyectos.
Los administradores profesionales de proyectos no sólo tienen habilidades en los aspectos técnicos del cálculo de cuestiones como el inicio y la conclusión antes de tiempo, también las habilidades interpersonales relacionadas con la motivación son importantes. Además, la capacidad para resolver confl ictos, cuando en el proyecto se presentan puntos críticos que requieren tomar decisiones, también es una habilidad fundamental. No cabe duda que dirigir proyectos exitosos será el mejor camino para demostrar a las personas que deciden los ascensos que usted está preparado para uno. Casi todo el trabajo de un proyecto se hace en equipo y dirigir un proyecto implica liderar a un equipo. Su éxito en la dirección de un proyecto se extenderá velozmente a los individuos del equipo. A medida que las organizaciones se vayan volviendo más planas (en razón de la reingeniería, el adelgazamiento y la subcontratación), la ejecución del trabajo, ese que antes se manejaba dentro de los departamentos, dependerá cada vez más de proyectos y de los líderes de esos proyectos.
martes, 20 de abril de 2021
EL IPOD DE APPLE TIENE SU PROPIO EQUIPO DE DESARROLLO DEL PRODUCTO Parte 2
La mayor parte del material de este capítulo aborda aspectos técnicos de la administración de proyectos (la estructuración de la red de un proyecto y el cálculo de la ruta crítica), pero, como se observa en el caso inicial, no cabe duda que los aspectos administrativos también tienen enorme importancia. El éxito de la administración de un proyecto es en gran medida una actividad que requiere de un cuidadoso control de los recursos críticos. En este libro se dedica mucho tiempo a hablar de la administración de recursos no humanos, como las máquinas y los materiales, sin embargo, el recurso fundamental para los proyectos suele ser el tiempo de los empleados. Los recursos humanos muchas veces son lo más caro, y las personas implicadas en los proyectos son críticos para el éxito de la empresa, y, con frecuencia, los más valiosos son los administradores, los asesores y los ingenieros.
La administración en los niveles más altos de una organización suele realizar malabarismos con una cartera de proyectos. Hay muchos tipos diferentes de proyectos, desde la creación de productos enteramente nuevos, las revisiones de productos viejos y los nuevos planes de marketing, hasta toda una serie de proyectos para servir mejor a los clientes y para reducir los costos.
Casi todas las compañías manejan los proyectos en forma individual, empujando cada uno de ellos para que pase por la tubería con la mayor velocidad y efi ciencia de costos posibles. Muchas de estas mismas compañías son muy buenas para aplicar las técnicas que se describen en este capítulo de modo que innumerables tareas son desempeñadas impecablemente, pero los proyectos no siempre presentan los resultados esperados. Es peor, muchas veces ocurre que los proyectos que consumen la mayor cantidad de recursos son los que tienen menos relación con la estrategia de la empresa.
Dentro del cuadro general, la decisión vital es qué mezcla de proyectos es más conveniente para la organización. Una empresa debe tener la mezcla correcta de proyectos que apoye mejor su estrategia. La compañía debe seleccionar los proyectos de entre las clases siguientes: derivados (cambios incrementales, como nuevos empaques de los productos o versiones sin adornos), innovaciones (cambios mayores que crean mercados enteramente nuevos) y plataformas (mejoras fundamentales aplicadas a los productos existentes). Los proyectos se pueden clasifi car en cuatro áreas básicas: cambio en el producto, cambio en el proceso, investigación y desarrollo, y alianza y asociación (véase la ilustración 3.1).
jueves, 8 de abril de 2021
EL IPOD DE APPLE TIENE SU PROPIO EQUIPO DE DESARROLLO DEL PRODUCTO
martes, 30 de marzo de 2021
PROGRAMACIÓN LINEAL UTILIZANDO EXCEL DE MICROSOFT - BIBLIOGRAFÍA SELECCIONADA
Anderson, D.R., D.J. Sweeney y T.A. Williams. An Introduction to Management Science, 11a. ed. Mason, OH. South-Western, 2005.
Kelly, Julia y Curt Simmons. The Unoffi cial Guide to Microsoft Excel 2007. Nueva York: John Wiley & Sons, 2007.
Winston, W.L. y S.C. Albright. Practical Management Science. 3a. ed. Mason, OH: South-Western, 2006.
miércoles, 24 de marzo de 2021
PROGRAMACIÓN LINEAL UTILIZANDO EXCEL DE MICROSOFT - Problemas Parte 7
10. Una agricultora de Wood County tiene un terreno de 900 acres. Piensa sembrar cada acre con maíz, soya o trigo. Cada acre con maíz produce 2 000 dólares de utilidad, cada acre con soya produce 2 500 dólares de utilidad y cada acre con trigo produce 3 000 dólares de utilidad. Ella tiene 100 trabajadores y 150 toneladas de fertilizante. La tabla que se presenta a continuación muestra los requerimientos por acre para cada una de las tres cosechas. Suponga una relación lineal y use Solver de Excel con el fin de determinar la mezcla óptima para sembrar maíz, soya y trigo para maximizar su utilidad.
martes, 23 de marzo de 2021
PROGRAMACIÓN LINEAL UTILIZANDO EXCEL DE MICROSOFT - Problemas Parte 6
lunes, 22 de marzo de 2021
PROGRAMACIÓN LINEAL UTILIZANDO EXCEL DE MICROSOFT - Problemas Parte 5
7. Quiere preparar un presupuesto que optimice el uso de una fracción de su ingreso disponible. Cuenta con un máximo de 1 500 dólares al mes para asignar a comida, vivienda y entretenimiento. La cantidad que gaste en alimento y vivienda juntos no debe pasar de 1 000 dólares. La cantidad que gaste sólo en vivienda no puede pasar de $700. El entretenimiento no puede pasar de $300 al mes. Cada dólar que gaste en comida tiene un valor de satisfacción de 2, cada dólar que gaste en vivienda tiene un valor de satisfacción de 3 y cada dólar que gaste en entretenimiento tiene un valor de satisfacción de 5.
Suponiendo una relación lineal, utilice Solver de Excel para determinar la asignación óptima de sus fondos.
8. La cervecería C-town produce dos marcas: Expansion Draft y Burning River. Expansion Draft tiene un precio de venta de $20 por barril, mientras que Burning River tiene un precio de venta de 8 dólares por barril. La producción de un barril de Expansion Draft requiere 8 libras de maíz y 4 libras de lúpulo. La producción de un barril de Burning River requiere de 2 libras de maíz, 6 libras de arroz y 3 libras de lúpulo. La cervecería tiene 500 libras de maíz, 300 libras de arroz y 400 libras de lúpulo. Suponga una relación lineal y use Solver de Excel para determinar la mezcla óptima de Expansion Draft y Burning River que maximice el ingreso de C-town.
viernes, 5 de marzo de 2021
PROGRAMACIÓN LINEAL UTILIZANDO EXCEL DE MICROSOFT - Problemas Parte 4
5. Resuelva el problema 4 añadiendo la restricción de que la dieta sólo puede contener un máximo de 150 calorías de grasa y que el precio del alimento A ha subido a 1.75 dólares la libra y el alimento B a 2.50 dólares la libra.
6. Logan Manufacturing quiere mezclar dos combustibles, A y B, para minimizar el costo de sus camiones.
Necesita un mínimo de 3 000 galones para sus camiones durante el mes entrante. Tiene una capacidad máxima de almacenamiento de combustible de 4 000 galones. Hay disponibles 2 000 galones del combustible A y 4 000 galones del combustible B. La mezcla de combustible debe tener un octanaje de un mínimo de 80.
Cuando se mezclan los combustibles, la cantidad obtenida es tan sólo igual a la suma de las cantidades que se vierten en la mezcla. El octanaje es el promedio ponderado de los octanos individuales, ponderados en proporción con sus respectivos volúmenes.
Se sabe lo siguiente. El combustible A tiene 90 octanos y cuesta 1.20 dólares por galón. El combustible B tiene 75 octanos y cuesta 0.90 dólares por galón.
a) Escriba las ecuaciones que expresan esta información.
b) Resuelva el problema utilizando Solver de Excel, proporcionando la cantidad de cada combustible que se usará. Plantee los supuestos necesarios para resolver este problema.
sábado, 27 de febrero de 2021
PROGRAMACIÓN LINEAL UTILIZANDO EXCEL DE MICROSOFT - Problemas Parte 3
4. Se está preparando la dieta para los dormitorios de la Universidad de Arizona. El objetivo es alimentar a los estudiantes al costo mínimo, pero la dieta debe contener entre 1 800 y 3 600 calorías. La dieta debe tener un máximo de 1 400 calorías de almidones y un mínimo de 400 de proteína. La dieta estará compuesta por dos alimentos: A y B. El alimento A cuesta 0.75 dólares por libra y contiene 600 calorías, 400 de ellas de proteína y 200 de almidones. No se pueden utilizar más de dos libras del alimento A por estudiante. El alimento B cuesta 0.15 dólares por libra y contiene 900 calorías, de las cuales 700 son de almidones, 100 de proteína y 100 de grasa.
a) Escriba las ecuaciones que representan esta información.
b) Resuelva gráficamente el problema indicando las cantidades de cada alimento que se deben usar.
Respuesta
4. a) 600A + 900B < 3 600
600A + 900B > 1 800
200A + 700B < 1 400
400A + 100B > 400
A < 2
Minimizar 0.75A + 0.15B
b) A = 0.54
B = 1.85
Obj = 0.68
martes, 23 de febrero de 2021
PROGRAMACIÓN LINEAL UTILIZANDO EXCEL DE MICROSOFT - Problemas Parte 2
3. Una compañía manufacturera ha descontinuado la producción de una línea de productos que no era rentable. Por ello, se ha creado un exceso considerable de capacidad de producción. La gerencia está considerando la posibilidad de dedicar este exceso de capacidad a uno o más de tres productos: X1, X2 y X3.
Las horas máquina requeridas por unidad son:
a) Plantee las ecuaciones que se pueden resolver para maximizar la utilidad por semana.
b) Resuelva las ecuaciones utilizando Solver de Excel.
c) ¿Cuál es la solución óptima? ¿Qué cantidad de cada producto se debería fabricar y cuál sería la utilidad resultante?
d) ¿Cuál es la situación en lo que respecta a los grupos de máquinas? ¿Se utilizaría toda la capacidad o habría tiempo disponible sin usar? ¿X3 estará a su capacidad máxima de ventas?
e) Suponga que se pueden obtener 200 horas adicionales por semana de los molinos trabajando horas extra. El costo incremental sería 1.50 dólares por hora. ¿Recomendaría que se hiciera? Explique cómo llegó a su respuesta.
domingo, 14 de febrero de 2021
PROGRAMACIÓN LINEAL UTILIZANDO EXCEL DE MICROSOFT - Problemas Parte 1
1. Resuelva el problema siguiente con Solver de Excel:
Maximizar Z = 3X + Y.
12X + 14Y ≤ 85
3X + 2Y ≤ 18
Y ≤ 4
2. Resuelva el problema siguiente con Solver de Excel:
Minimizar Z = 2A + 4B.
4A + 6B ≥ 120
2A + 6B ≥ 72
B ≥ 10
Respuesta: 2. La combinación óptima es B = 10, A = 15 y Z = 70.
martes, 9 de febrero de 2021
PROGRAMACIÓN LINEAL UTILIZANDO EXCEL DE MICROSOFT - PROBLEMA RESUELTO 2 - Solución - Paso 6: Resuelva el problema Haga clic en Resolver. Parte 2
La segunda respuesta requerida era si valía la pena pagar a un proveedor de urgencia 1 dólar por cada unidad adicional de panes. El informe de respuestas muestra que la restricción de los panes era vinculante.
Esto significa que si hubiera más panes se podría ganar más dinero. No obstante, el informe de respuestas no indica si este pedido extraordinario de panes a 1 dólar la unidad vale la pena. Para responder la pregunta, se tiene que ver el informe de sensibilidad.